Have you ever wondered why competing physical stores locate themselves close to each other as a cluster? Since we live in the AnyLogic world, we will use simulations and artificial intelligence to analyze this mystery, but this question is a classical Game Theory problem, so let’s start by discussing this from a game theory perspective that will give us the theoretical grounds to develop a simulation model.
Game Theory Perspective
Let’s imagine two competitors soon to open a new store in a community in which customers are uniformly distributed in terms of location and interest for the product sold. If the stores cooperate with each other, they can locate themselves in positions that minimizes the average distance travelled by a customer, while at the same sharing 50% of the demand. This collaborative scenario is a social optimal solution and everybody would be happy with it.
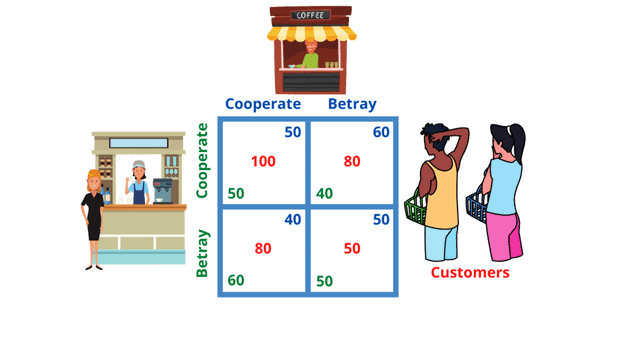
But after they give each other a handshake and chose the location of their respective stores, each one individually can decide to either cooperate, or betray. This can be represented by a table that shows the rewards of each store owner based on the decision they both make, alongside with the reward for the customers.
If they both cooperate, each gets 50% of the customers, and the customers get maximum reward.
If only one of them betrays, moving to the center of the city, it gets 60% of the customers and some customers have to travel more, reducing the customer reward to 80.
If they both betray each other moving to the center of the city, they still get 50% of the customers but the social reward is at its lowest since people living in the edges of the city now have to travel more.
If a store owner thinks about their own benefit, the following strategic mindset is presented.
- If the other store cooperates, the maximum reward will be obtained by betraying.
- If the other store betrays, the maximum reward will be obtained by betraying.
From this perspective, it is always a better strategy to betray, as long as the store owner doesn’t care about social happiness. Both betraying each other is the Nash Equilibrium of the system.
This is of course a simplified version of the world since it doesn’t consider the fact that they might lose customers by being too far, and we also don’t consider the psychology of the human mind in these scenarios.
Simulation Model
Ok, now that we covered the context, let’s try to find a way to make this happen in a simulation setup using AnyLogic. To do that, we need a business that is able to make decisions based on its own selfish interests; but this is not so simple to conceptualize if there are several stores in a big city with lots of customers. So, to avoid getting into the trouble of making an algorithm ourselves, we can use reinforcement learning (RL) with a reward equal to the number of sales made. This reward will create selfish businesses who don’t care about social optimization, but only about their own financial benefit, which is fine because that’s how store owners behaved in the game theory example.
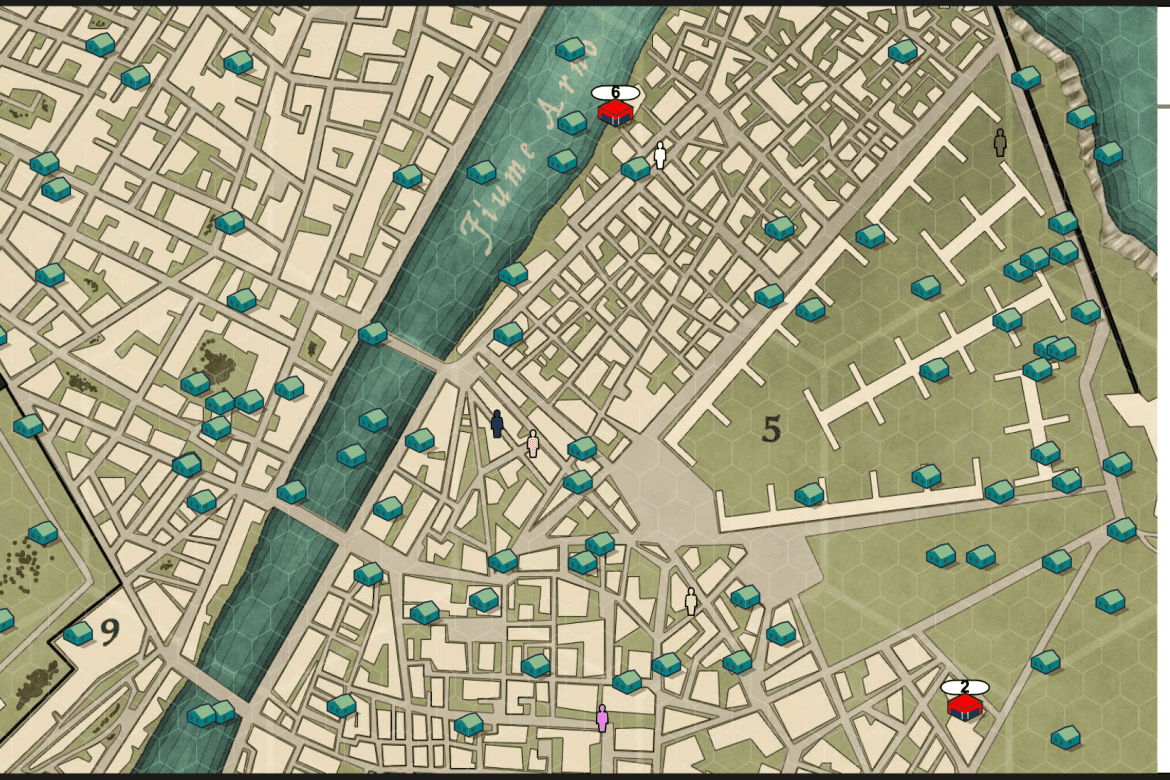
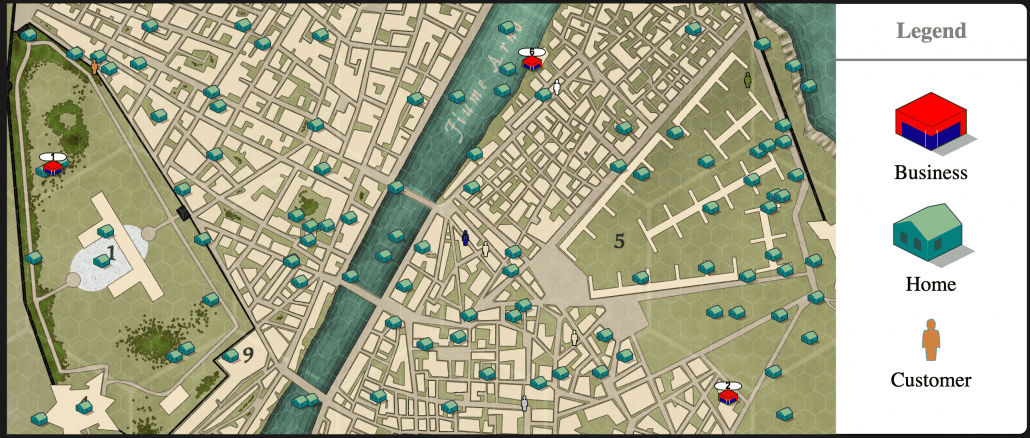
The city is simplified to be a rectangular area with businesses and houses randomly placed somewhere in that area. Each house has a random number of customers inside it. When a customer needs a product (which is decided by a simple rate of 1 every arbitrary time unit), they will move to the closest business and will always go back home with the product in their hands.
So, with the general model created, now we need to make it RL-ready, and if you are familiar with RL, you know that we need to create an observed space, an action space and a reward. Let’s see each one of them separately.
Observations
In all the following observations, you have a variable called performingAgent, which is equivalent to the id of the agent making the decisions. This is important since only 1 agent will be making decisions during the training while the others remain in fixed places (I will explain this further later).
So, these are the observations:
- The position of all the homes in the city with a normalized coordinate ranging from 0 to 1

- The normalized number of people in each home. 0 if there’s only 1 person, and 1 if there

- The normalized coordinates of the other businesses.

- The normalized coordinates of the business that is making an action.

Reward
A reward of 1 is obtained every time a sale is made.
Action
Nine actions are defined: four of them are related to movements parallel to x and y axes, four of them to movements in diagonal and the last action is not to move at all. The distance moved by the agent after each action is fixed and arbitrarily chosen.
Training using Pathmind
As of the writing of this article, Pathmind doesn’t have a feature that allows independent trainings for multiple agents that are competing with each other with different and independent reward systems, so what we need to do, as previously explained, is to train one individual business while maintaining the others in a fixed position (or moving randomly). And if we want to use a competition setup with n competitors, we need to train the model, with an initial configuration that defines which business is going to make the decisions. We do this with a random variable as follows (representing the performingAgent parameter we talked about before):
This is important for the training to work, because you need the agent to have a sense of self, based on its id. So, the model you will find in the cloud (see references at the end for the link) is the test environment, and not the training environment because we want to train agents individually with selfish behavior and not as a group, meaning that for training purposes, the number of controlled agents is only 1, but for testing purposes, the number of controlled agents can be higher.
Conclusions
What we find using RL for this problem is that the businesses, have a constant incentive to move closer and closer to the other businesses as the best strategy to land more sales. And the position in which these businesses will cluster is close to the “center of mass” of the available customers within the city, which is near the city center if the house locations and customers per house are uniformly distributed.
Which is great about this example is that we have found the Nash equilibrium using simulations and RL without any incentive other than sales, meaning that you can solve other very simple problems using RL without a lot of Research & Development efforts.
Homework
I can’t finish this article without a homework for you to try. Imagine now a new situation in which businesses care about the social optimization and want to collaborate in order to have similar sales, while at the same time minimizing the distance travelled by customers. How would you do this? Would you still use Reinforcement Learning? Would you rather use the optimization experiment or your own optimization algorithm? Or maybe some other clever solution? If you do this homework share your AnyLogic Cloud solution in the comments section.
You can check and download this model directly through the AnyLogic cloud link:
https://cloud.anylogic.com/model/8cc811f3-b7a4-48ff-9a01-0e4f5b8e76b7?mode=SETTINGS.
For more details on the topic, watch the video available in the YouTube Noorjax Consulting channel:
[https://www.youtube.com/watch?v=9JWZeQ9Pdzk ]