It’s generally a good idea to reduce the number of parameters of your optimization problem, and sometimes it feels that your problem needs hundreds of them. But does it? How can you reduce those dimensions without affecting the final solution? And in AnyLogic in particular, using the demo version of the optimization experiment, you are forced to do so since the limit of parameters is 7.
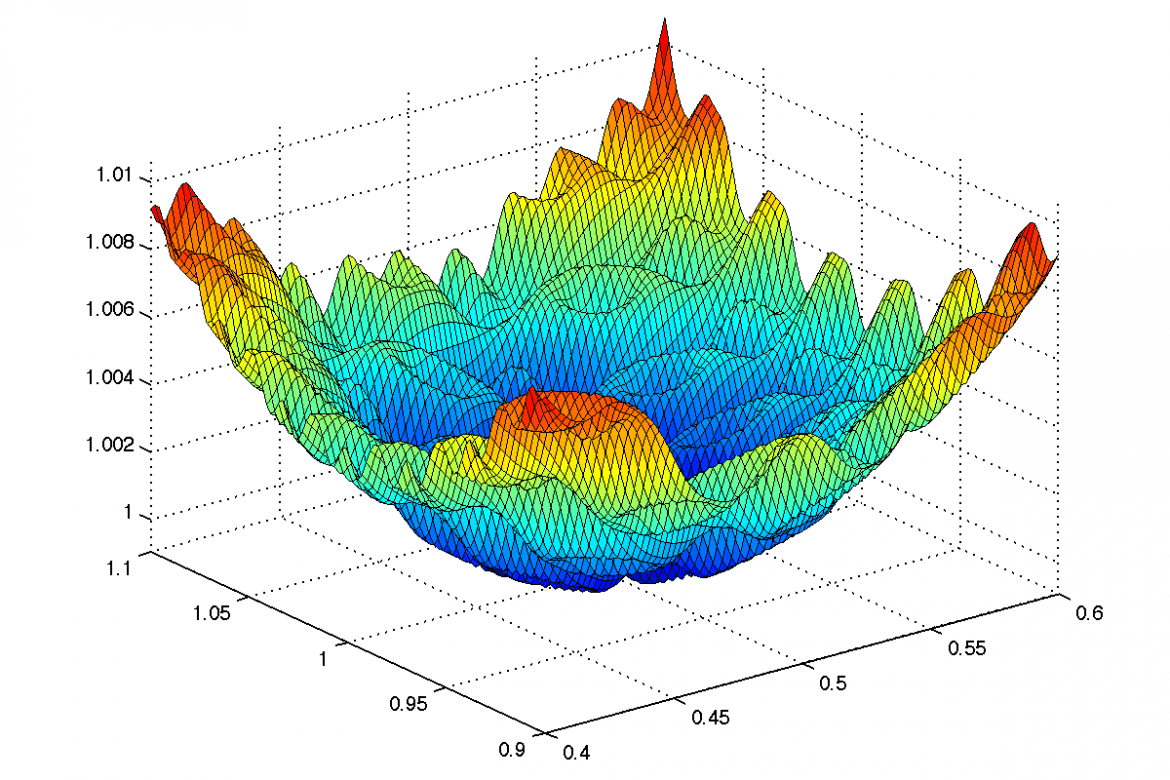
There is some art present into defining an optimization problem that requires a little bit of creativity. Non-linear optimization problems use heuristics to find an optimal solution. These heuristics go to random places in your optimization landscape and if a good solution is found, a search on the vicinity of that solution is performed. This means that any parameter you choose that simplifies your problem needs to have vicinity points that are similar.
Example
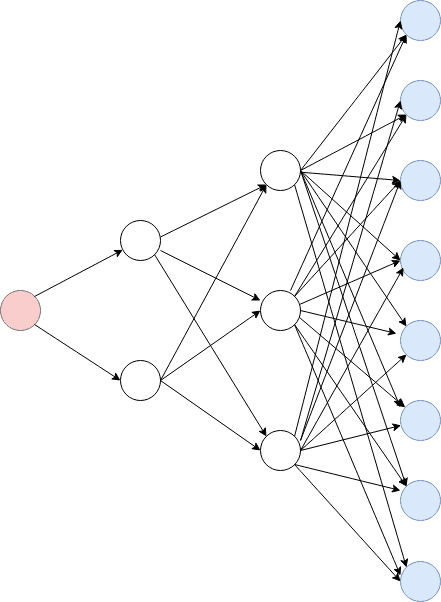
For instance, let’s imagine a problem in which you have to minimize your costs by sending inventory through a tree shaped structure and you have to define what route to take assuming that each blue node receives products from the red node following a defined set of unique routes. Also each blue node has a certain demand to be fulfilled.
This can be defined in many ways. One way is to generate percentages for each potential path. For instance from the red node, the products can be distributed through 2 different routes towards the second level of nodes. This is equivalent to one parameter (% of products going to the first node of the second level). If we use the same logic for the next levels, the second level has 4 parameters to be defined and the third level has 21 parameters to be defined, making a total of 27.
How to reduce the number of parameters significantly? One option is to define priorities for each blue node and instead of using percentages of distribution from left to right, defining priorities for each blue node in order to request products from different nodes according to their demand. The priorities will define who asks for products first, and there are 8 nodes, which is equivalent to 8! permutations. This 8! permutations (40,320) can be coded as a unique number from 0 to 40319, where each one of these numbers represents a permutation, and this is the number that will be used as a parameter for the optimization problem. The same can be done with the second (2 permutations) and third level (6 permutations) of the network, hence reducing the number of parameters used from 27 to 3 without affecting the result of the optimization, and probably increasing the performance.
Conclusion
Defining an optimization problem with its constraints and requirements is difficult. And reducing the number of variables is an art that requires creativity, experience and an overall understanding on how the heuristics of the optimization algorithms work.




All Comments:
Hi,
is the number of parameters for the optimization experiment only restricted for the Evaluation version of AnyLogic or also for the full version?
it’s only restricted for the evaluation version